petri net

Petri nets enable the analysis, modeling and simulation of dynamic systems with concurrent and non-deterministic processes. Petri nets are named after the German mathematician Carl Adam Petri, who introduced them in 1962.

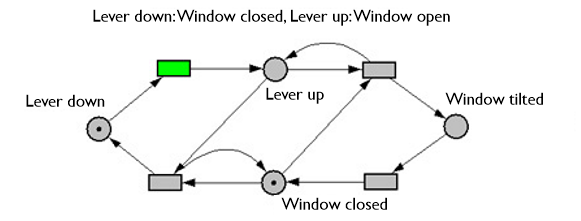
Formally, a Petri net corresponds to specific mathematical structures that are axiomatically based. Accordingly, a Petri net is a directed, marked bichromatic graph.

• Graph, as a set of points connected among them, where the connections are called edges.
• Directed, because the edges of the graph are assigned a direction, thereby defining the type of connection between the nodes.
• Bichromatic (term from graph theory), because there are two well-differentiated types of nodes in a Petri net; i.e. places for states (= preconditions) of a system and transitions for the events (= activities).

The static structure of a Petri net is thus described by directed edges (arrows), places (circles) and transitions (bars). The directed edges always connect

• an event with a state, i.e. with the occurrence of the event the respective state is realized or else
• a state with an event, i.e. with the realization of the state the event can occur.

However, events or states are never directly connected to each other by a directed edge.

A Petri net does not contain isolated nodes, parallel edges or doubly directed edges.

The dynamic behavior of Petri nets, i.e. the realization of other states, is made visible with the help of the so-called marking (of states) and its variability caused by switching rules. A place is called marked if there are one or more marks ( black dots) on it. A transition can switch - i.e. the transition is active - and the event represented by it can occur if all its predecessor places contain at least one mark. If a transition switches - i.e., the event occurs - one token is removed from each of the predecessor places and one additional token is assigned to each of the successor places. Important aspects with respect to the dynamics of a network are:

• Safety: A Petri net is said to be safe if no state of the net can be assigned more than one mark at each reachable mark,
• Liveness: A transition is alive if it is activated after finitely many admissible switching operations and can thus switch. A Petri net is alive if all its transitions are alive without exception.
• Deadlock: A Petri net has a deadlock (blockade) if a state situation is realized by finitely many switching operations which do not activate a single transition.

Depending on the attributes of the tokens, a distinction is made between conditional and event nets, place and transition nets, and higher Petri nets.